Usar un software de mantenimiento para la gestión de flotas es, sin lugar a dudas, una de las mejores decisiones estratégicas que se pueden asumir en coherencia con la gerencia.
Cualquier software de gestión de mantenimiento debe ser una herramienta valiosa para las empresas que buscan optimizar sus operaciones de mantenimiento. Uno de los beneficios más importantes es la mejora en la planeación y programación. Debes ser capaz de planificar y programar los mantenimientos con anticipación, evitando retrasos y reduciendo los tiempos de inactividad de los vehículos. Esto es especialmente importante en industrias como la logística y el transporte, donde la disponibilidad de los vehículos es crucial para el éxito de la empresa. Además, la planeación y programación efectiva también puede ayudar a reducir costos y mejorar la eficiencia de los procesos.
Otro beneficio importante es la mejora en la toma de decisiones. El software de gestión de mantenimiento debe proporcionar información detallada sobre los activos y los procesos para que los gerentes puedan tomar decisiones informadas sobre cómo manejar sus activos. Esto puede incluir decisiones sobre cuando reemplazar un componente, cómo asignar recursos y cómo optimizar los procesos. Con esta información, los gerentes pueden identificar oportunidades para reducir costos y mejorar la eficiencia, lo que puede tener un impacto significativo en el éxito de la empresa.
La reducción de costos es otro beneficio importante del software de gestión de mantenimiento. Al monitorear el progreso de los mantenimientos y los costos asociados, las empresas pueden identificar oportunidades para reducir gastos y optimizar sus procesos de mantenimiento. Esto puede incluir la identificación de componentes que no son esenciales para el funcionamiento del vehículo, la optimización de los procesos de mantenimiento y la reducción de los costos de repuestos. Además, la reducción de costos también puede ayudar a mejorar la eficiencia y la productividad de los empleados, lo que puede tener un impacto positivo en la cultura de la empresa.
Proyecto optimización de mantenimiento
Crearemos un modelo que proyecte el calendario de mantenimiento óptimo para una flota de \(m\) unidades y \(H\) periodos de tiempo. El mantenimiento se refiere a cuándo debe ocurrir y cuántas horas de funcionamiento se planean para cada unidad en cada período de tiempo. Las unidades \(i\) y los periodos de tiempo \(t\) se representan mediante conjuntos.
\[i ∈ \{1,2,...,m\}\]
y
\[ t ∈ \{1,2,...,H\} \]
En primer lugar, se utilizan dos variables para definir un calendario. Una variable binaria que almacena el mantenimiento planeado.
\[ y_{i,t}=\cases{1, \text{si se realiza mantenimiento de la unidad i en el tiempo t}\\0, \text{de lo contrario}} \]
Y una variable \(x_{i,t} ≥ 0\) que representa el número de horas de funcionamiento para la unidad \(i\) en el período de tiempo \(t\).
Para encontrar un calendario de mantenimiento óptimo para una flota, se escribe un MILP (Programación Lineal Entera Mixta) donde el objetivo es minimizar el número de ocasiones de mantenimiento planeadas, es decir, minimizar la suma de \(y_{i,t}\) sobre cada unidad \(i\) y período de tiempo \(t\). Para el programa principal, las restricciones incluidas son una demanda de tiempo de funcionamiento para la flota completa de \(D\) horas y requisitos de mantenimiento después de al menos \(U_i\) tiempo periodos o \(T_i\) horas de funcionamiento desde el último mantenimiento, lo que sea lo primero. Esto se puede escribir como:
\[ min \sum_{i=1}^{m}\sum_{t=1}^{H}y_{i,t} \]
\[ \text{sujeto a } \sum_{i=1}^{m}\sum_{t=1}^{H}x_{i,t}\ge D, \]
\[ \sum_{j=\tau}^{\tau+U_i}y_{i,t} \ge 1, \quad ∀i, \tau ∈ \{1,2,...,H-U_i\}, \]
\[ \sum_{j=t}^{t+u}x_{i,t}\le T_i+T_i \sum_{j=t}^{t+u}y_{i,t}, \quad ∀i, t, u ∈ \{0,1,...,H-t\}, \]
\[ x_{i,t} + x^{max}y_{i,t} \le x^{max}, \quad ∀i, t, \]
\[ x_{i,t} \ge 0, \quad ∀i, t, \]
\[ y_{i,t} ∈ \{0,1\}, \quad ∀i,t, \]
Donde Eq.2 garantiza que se cumple la demanda de horas de funcionamiento y Eq.3 y Eq.4 manejan las restricciones de mantenimiento. La restricción Eq.5 garantiza que no se planean operaciones para una unidad que está en mantenimiento, es decir, fuerza la deducción:
\[ y_{i,t}=1 ⟶ x_{i,t}=0, \quad ∀i, t. \]
El parámetro \(x^{max}\) es el límite superior de \(x_{i,t}\), que se establece en \(744\) horas, ya que ese es el máximo número de horas que un mes puede tener.
Restricción de programación de mantenimiento según calendario
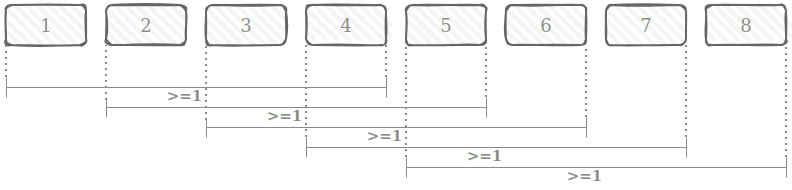
La Eq.3 controla que el mantenimiento se realice al menos después de \(U_i\) periodos de tiempo desde el último mantenimiento. Esta restricción establece que para la suma de \(y_{i,t}\) dentro de todos los periodos de tamaño \(U_i + 1\), al menos uno de los periodos tiene que tener un evento de mantenimiento planeado con \(y_{i,t} = 1\), según el requisito de mantenimiento basado en calendario. Para visualizar las restricciones, se muestra un ejemplo para una unidad \(j\) con \(U_j = 3\) y \(H = 8\).
Restricción de programación de mantenimiento según uso
La restricción Eq.4 se compone de la suma del tiempo de funcionamiento, operación o funcionamiento,
\[ \sum_{j=t}^{t+u}x_{i,t}, \quad ∀i, t, u ∈ \{0,1,...,H-t\}, \] y la suma de eventos de mantenimiento
\[ \sum_{j=t}^{t+u}y_{i,t}, \quad ∀i, t, u ∈ \{0,1,...,H-t\} \]
sobre todos los periodos de tiempo continuos de diferentes tamaños. Para cada evento de mantenimiento en el período, se agregan \(T_i\) unidades de tiempo dentro del área aceptable de tiempo de funcionamiento. Por lo tanto, la restricción se escribe como: \[ \sum_{j=t}^{t+u}x_{i,t}\le T_i+T_i \sum_{j=t}^{t+u}y_{i,t}, \quad ∀i, t, u ∈ \{0,1,...,H-t\}, \]
Los periodos desde \(t\) hasta \(t + u\) se visualizan en la Figura 2 para una unidad y \(H = 6\).
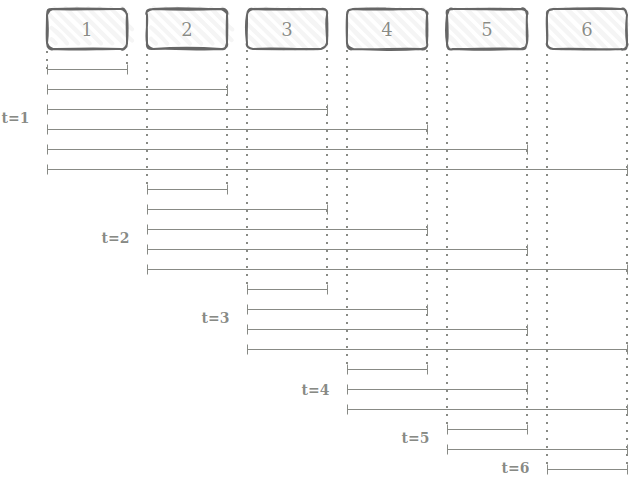
Las ecuaciones de la restricción Eq.4 escritas son:
\[ x_{i,1} \le T_i+T_iy_{i,1} \]
\[ x_{i,1} + x_{i,2}\le T_i+T_iy_{i,1} + T_iy_{i,2} \]
\[ x_{i,1} +x_{i,2} +x_{i,3}\le T_i+T_iy_{i,1} +T_iy_{i,2}+T_iy_{i,3} \]
\[ ⠇ \]
\[ x_{i,1} +x_{i,2} +...+x_{i,H}\le T_i+T_iy_{i,1} +T_iy_{i,2}+...+T_iy_{i,H} \]
\[ x_{i,2} \le T_i+T_iy_{i,2} \]
\[ x_{i,2} + x_{i,3}\le T_i+T_iy_{i,2} + T_iy_{i,3} \]
\[ x_{i,2} +x_{i,3} +x_{i,4}\le T_i+T_iy_{i,2} +T_iy_{i,3}+T_iy_{i,4} \]
\[ ⠇ \]
\[ x_{i,2} +x_{i,3} +...+x_{i,H}\le T_i+T_iy_{i,2} +T_iy_{i,3}+...+T_iy_{i,H} \]
\[ ⠇ \]
\[ x_{i,H-1} \le T_i+T_iy_{i,H-1} \]
\[ x_{i,H-1} + x_{i,H}\le T_i+T_iy_{i,H-1} + T_iy_{i,H} \]
\[ x_{i,H} \le T_i+T_iy_{i,H} \]
para cada unidad \(i\).
Ejemplo
Un pequeño ejemplo del modelo descrito, con valores de parámetros de entrada listados en la Tabla No.1, se resuelve:
| Parámetro | Valor |
|---|---|
| \(m\) | 2 |
| \(H\) | 8 |
| \(D\) | 480 |
| \(U_i\) | c(3, 3) |
| \(T_i\) | c(90, 90) |
El número total de horas de operación para la solución es:
\[ \sum_{i=1}^{m}\sum_{t=1}^{H}x_{i,t}^{*}=D, \]
las horas máximas de funcionamiento y los periodos de tiempo entre mantenimientos son iguales a \(T_i\) y \(U_i\) ,respectivamente, y el número de eventos de mantenimiento es:
\[ y_{tot}^{*}=\sum_{i=1}^{m}\sum_{t=1}^{H}y_{i,t}^{*}=4 \]
Es claro que el problema planteado aquí es en extremo básico, y seguramente no se ajusta a cualquiera que sea tu necesidad. Pero, en mi defensa, mi intención es mostrar que no es imposible crear un servicio en la nube para lograr optimizar los recursos que se encuentran bajo tu control y administración.
Cómo citar
@online{chiquito_valencia2025,
author = {Chiquito Valencia, Cristian},
title = {Gestión de Sistemas de Mantenimiento},
date = {2025-01-27},
url = {https://cchiquitovalencia.github.io/posts/2025-01-27-maintenance_management/},
langid = {en}
}