# Definir la función objetivo
objective_function <- function(vector) {
return(sum(vector^2))
}
# Generar un número aleatorio en el intervalo [min, max]
rand_in_bounds <- function(min, max) {
return(min + ((max-min) * runif(1)))
}
# Generar un vector aleatorio en el espacio de búsqueda
random_vector <- function(minmax) {
#minmax <- matrix(bounds,nrow = problem_size, ncol = problem_size, byrow = FALSE)
return(runif(length(minmax), min = minmax[,1], max = minmax[,2]))
}
# Dar un paso en una dirección aleatoria
take_step <- function(minmax, current, step_size) {
position <- numeric(length(current))
for (i in 1:(length(current)/problem_size)) {
min <- max(minmax[i,1], current[i]-step_size)
max <- min(minmax[i,2], current[i]+step_size)
position[i] <- rand_in_bounds(min, max)
}
return(position)
}
# Dar un paso grande en una dirección aleatoria
large_step_size <- function(iter, step_size, s_factor, l_factor, iter_mult) {
if (iter > 0 && iter %% iter_mult == 0) {
return(step_size * l_factor)
} else {
return(step_size * s_factor)
}
}
# Dar un paso y un gran paso en direcciones aleatorias
take_steps <- function(bounds, current, step_size, big_stepsize) {
step <- list()
big_step <- list()
step$vector <- take_step(bounds, current$vector, step_size)
step$cost <- objective_function(step$vector)
big_step$vector <- take_step(bounds, current$vector, big_stepsize)
big_step$cost <- objective_function(big_step$vector)
return(list(step, big_step))
}
# Inicializar un dataframe para almacenar los resultados
results <- data.frame(iteration = integer(), cost = numeric())
# Realizar la búsqueda aleatoria adaptativa
search <- function(max_iter, bounds, init_factor, s_factor, l_factor, iter_mult, max_no_impr) {
step_size <- (bounds[1,2]-bounds[1,1]) * init_factor
current <- list()
current$vector <- random_vector(bounds)
current$cost <- objective_function(current$vector)
count <- 0
for (iter in 1:max_iter) {
big_stepsize <- large_step_size(iter, step_size, s_factor, l_factor, iter_mult)
steps <- take_steps(bounds, current, step_size, big_stepsize)
if (steps[[1]]$cost <= current$cost || steps[[2]]$cost <= current$cost) {
if (steps[[2]]$cost <= steps[[1]]$cost) {
step_size <- big_stepsize
current <- steps[[2]]
} else {
current <- steps[[1]]
}
count <- 0
} else {
count <- count + 1
if (count >= max_no_impr) {
step_size <- step_size / s_factor
count <- 0
}
}
# Almacenar los resultados en el dataframe
results <<- rbind(results, data.frame(iteration = iter, cost = current$cost))
}
return(current)
}
# Configuración del problema
problem_size <- 2
bounds <- matrix(c(-5, 5), nrow = problem_size, ncol = 2, byrow = TRUE)
# Configuración del algoritmo
max_iter <- 100
init_factor <- 0.05
s_factor <- 1.3
l_factor <- 3.0
iter_mult <- 10
max_no_impr <- 30
# Ejecutar el algoritmo
best <- search(max_iter, bounds, init_factor, s_factor, l_factor, iter_mult, max_no_impr)Taxonomía
El algoritmo Adaptative Random Search pertenece al conjunto general de enfoques conocidos como Optimización Estocástica y Optimización Global.
Es un método de búsqueda directa, en el sentido de que no requiere derivadas para para navegar por el espacio de búsqueda. Adaptative Random Search es una extensión de los algoritmos Random Search.
Estrategia
El algoritmo Adaptative Random Search fue diseñado para abordar las limitaciones del tamaño de paso fijo en el algoritmo de Localized Random Search.
La estrategia de la Adaptative Random Search consiste en realizar paso óptimo necesario para alcanzar el óptimo global en el espacio de búsqueda. Esto se consigue probando y adoptando tamaños de paso menores o mayores sólo si mejoran el rendimiento de la búsqueda.
La estrategia del algoritmo Adaptive Step Size Random Search (la técnica específica revisada) consiste en probar un paso mayor en cada iteración y adoptarlo si mejora el resultado. Los pasos muy grandes se prueban de la misma manera, aunque con una frecuencia mucho menor. Esta estrategia de preferir movimientos grandes tiene por objeto permitir que la técnica escape a los óptimos locales. Los pasos más pequeños se adoptan si no se produce ninguna mejora durante un periodo prolongado.
Procedimiento

Heurística
Adaptative Random Search fue diseñado para dominios de problemas de optimización de funciones continuas.
Los candidatos con igual costo deben considerarse mejoras para permitir que el algoritmo progrese a través de mesetas en la superficie de respuesta.
Adaptative Random Search puede adaptar la dirección de búsqueda además del tamaño del paso.
El tamaño del paso puede adaptarse para todos los parámetros o para cada parámetro individualmente.
Código
En el ejemplo, el algoritmo se ejecuta durante un número fijo de iteraciones y devuelve la mejor solución candidata descubierta. El problema del ejemplo es un caso de optimización de una función continua que busca
\(min f(x)\) donde \(f = ∑_{i=1}^n X_i^2\), \(-5.0<=x_i<=5.0\) y \(n=2\).
La solución óptima para esta función es \((v_0,...,v_{n-1})=0.0\)
Revisamemos el comportamiento del algoritmo para encontrar la solución óptima:
library(ggplot2)
# Crear modificaciones al plot
crear_tema <- function() {
theme_minimal() +
theme(
plot.background = element_rect(fill = "white", color = NA),
panel.grid.major = element_line(color = "white", size = 0.2),
panel.grid.minor = element_line(color = "white", size = 0.2),
panel.background = element_rect(fill = "white", color = NA),
plot.title = element_text(face = "bold", size = 14, color = "#4d6080"),
axis.title = element_text(face = "bold", size = 12, color = "#4d6080"),
axis.text = element_text(size = 10, color = "#4d6080"),
axis.line = element_line(size = 1.5, colour = "#de6f41"),
legend.background = element_rect(fill = "#4d6080", color = NA),
legend.key = element_rect(fill = "grey90", color = NA),
axis.ticks.x = element_line(color = "#de6f41", size = 1),
axis.ticks.y = element_line(color = "#de6f41", size = 1)
)
}
ggplot(results, aes(x = iteration, y = cost)) +
geom_line() +
labs(title = "Progreso de la función objetivo",
x = "Iteración", y = "Costo")+
crear_tema()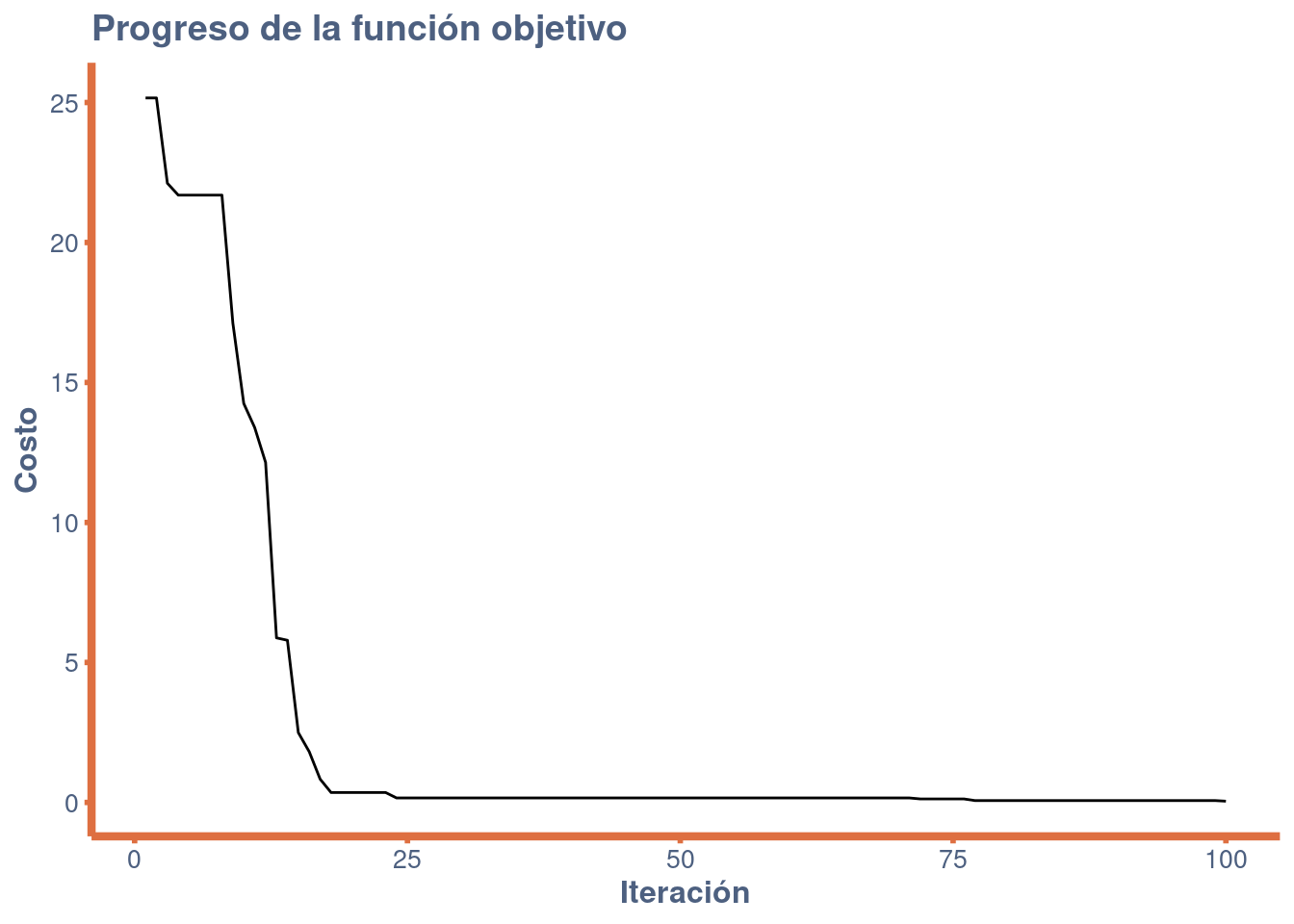
La solución óptima es entonces:
best$vector[1] 0.1144359 -0.1796417 0.0000000 0.0000000Cómo citar
@online{chiquito_valencia2023,
author = {Chiquito Valencia, Cristian},
title = {Adaptative {Random} {Search}},
date = {2023-11-13},
url = {https://cchiquitovalencia.github.io/posts/2023-11-13-adaptative_random_search/},
langid = {en}
}